Pavage à l’aide de gnomons
Petit exercice transmis par un de mes collègues à Marianne.
Je pense que c’est un exercice niveau “fin de lycée” qui donne un oeil neuf sur le raisonnement par récurrence.
Énoncé
Soit $n$ un entier supérieur à $1$. On s’intéresse au pavage du carré de longueur $2^n$, vu comme un damier composé de cases $1 \times 1$, dont on a retiré une des cases (n’importe laquelle). On appellera un tel damier damier percé de dimension $2^n \times 2^n$.
On souhaite donc montrer qu’il est possible de paver un damier percé à l’aide de tuiles que nous appellerons gnomons. Ici, un gnomon est une tuile formée de trois cases.
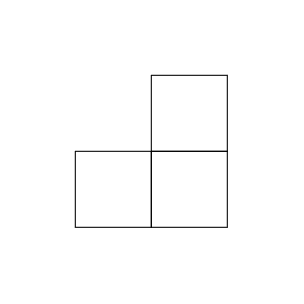
La question est donc la suivante: prouver qu’il est possible de paver n’importe quel damier percé de dimension $2^n \times 2^n$ à l’aide de gnomons. Paver signifie ici recouvrir entièrement les cases du damier, sans chevauchement de pièces.
Correction
On raisonne par récurrence sur $n$.
Si on suppose que $n = 1$, alors il suffit d’une tuile pour recouvrir n’importe quel damier percé $2 \times 2$ : une tel damier est exactement un gnomon.
On suppose que pour $n \in \mathbb{N}$, il est possible de paver un damier percé de dimension $2^n \times 2^n$. On souhaite alors montrer que l’on peut paver un damier percé de dimension $2^{n+1} \times 2^{n+1}$. On subdivise un tel damier en quatre quadrants de dimension $2^n \times 2^n$. Sans perte de généralités, on suppose que le “trou” est dans le quadrant en haut à gauche.

On peut donc utiliser l’hypothèse de récurrence sur le quadrant en haut à gauche : on pave ainsi ce quadrant en particulier. Reste à trouver un moyen de paver les trois quadrant restants.
Pour chacun d’entre eux, on utilise de nouveau l’hypothèse de récurrence. Et puisque, par hypothèse de récurrence, il nous est possible de paver un damier percé, nous allons ici paver chaque quadrant restant en laissant un trou bien choisi :

En laissant de tels emplacements libres, il y a exactement la place pour un dernier gnomon ! Ainsi, à l’aide de quatre applications de l’hypothèse de récurrence, on a montré l’existence d’un tel pavage pour un damier percé de dimension $2^{n+1} \times 2^{n+1}$.
Et on conclut ce raisonnement par récurrence.
